侧边栏壁纸
博主头像
Excalibur博主等级

真实自有万钧之力。

  • 累计撰写 25 篇文章
  • 累计创建 14 个标签
  • 累计收到 2 条评论
标签搜索
算法

地铁大小交路优化模型的遗传算法求解

Excalibur
Excalibur
2020-05-13 / 0 评论 / 0 点赞 / 304 阅读 / 7,732 字
温馨提示：
本文最后更新于 2022-04-07，若内容或图片失效，请留言反馈。部分素材来自网络，若不小心影响到您的利益，请联系我们删除。

1️⃣ 问题陈述

1️⃣.1️⃣ 需要解决的问题

  目前地铁一般采用如下的单一交路：
在这里插入图片描述目前，我国绝大多数城市都采用这种交路形式，但是当断面客流量分布不均匀时容易造成线路运能浪费，客流拥挤。

替代方案就是用大小交路：
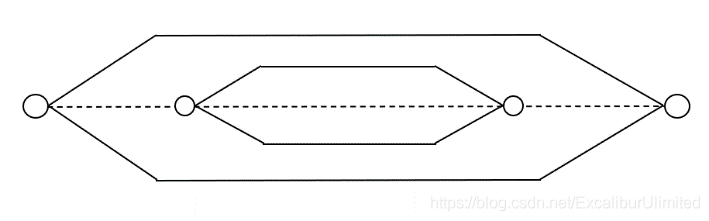
在这里插入图片描述
在这里插入图片描述
使用遗传算法程序就是在既定的OD矩阵下找到最优的大小交路的往返站$S_a,S_b$以及相应的大小交路的发车频率$f_1,f_2$，也就是在遗传算法每次运行中，根据不同的大小交路折返站的设置，划分预定的OD出行矩阵，然后计算目标函数，判断是否达到最优。

1️⃣.2️⃣ 变量定义

  • $Q_1$——出行$O$点或$D$点位于小交路覆盖区段外出行以及$OD$均位于小交路覆盖区段外的客流量，人；
  • $Q_2$——出行$OD$位于小交路覆盖区段的客流量，人；
  • $t_{1d}、t_{2d}$——$Q_1、Q_2$对应乘客的平均候车时间，$s$;
  • $q_$——在车站$o$上车，在车站$d$下车的客流量，人；
  • $i$——列车交路的集合，$i={1,2}$，$1$代表大交路，$2$代表小交路；
  • $f_i$——大小交路运行方式下的交路i的发车频率，对/小时；
  • $f$——单一交路运行方式下的发车频率，对/小时；
  • $f_$——最小发车频率，设置为$12$对/小时；
  • $T_{1周}、T_{2周}$——大小交路列车周转时间，$s$;
  • $t_{运,j}$——列车在区间$j$的纯运行时间，$s$；
  • $t_{停,j}$——列车在车站$h$的停站时间，$s$，设置为$30s$；
  • $t_{折}$——列车在终点站、中间站的最小折返间隔时间，$s$，设置为$120s$;
  • $C_z$——列车定员，即标准载客人数，人，设置为$1460$；
  • $\alpha$——列车满载率上限，设置为100%；
  • $I_o$——列车最小追踪间隔，$s$，设置为$120s$;

1️⃣.3️⃣ 目标函数

$$\min _{Z}=Q_{1} \cdot t_{1 d}+Q_{2} \cdot t_{2 d}$$

其中

$$Q_{1}=\sum_{d=1}^{n} \sum_{o=1}^{n} q_{o d}-Q_{2}\\Q_{2=} \sum_{d=o+1}^{b} \sum_{o=a}^{b-1} q_{o, d}+\sum_{d=a}^{o-1} \sum_{o=a+1}^{b} q_{o, d}$$ $$t_{2 d}=\frac{1}{2} \cdot \frac{60}{f_{1}+f_{2}}\\ \\t_{1 d}=\frac{1}{2} \cdot \frac{60}{f}$$

1️⃣.4️⃣ 约束条件

  • 列车数量
$$\left[\frac{T_{\text {周1}}}{60} \cdot f_{1}\right]+\left[\frac{T_{\text {周} 2}}{60} \cdot f_{2}\right] \leq\left[\frac{T_{\text {周} 1}}{60} \cdot f\right]$$

其中

$$T_{\text {周} 1}=2 \cdot\left(\sum_{j=1}^{n-1} t_{\text {运}},_{j}+\sum_{h=1}^{n} t_{\text {停, } h}+\sum t_{\text {折}}\right)\\T_{\text {周} 2}=2 \cdot\left(\sum_{j=a}^{b-1} t_{\text {运}},_{j}+\sum_{h=a}^{b} t_{\text {停, } h}+\sum t^{'}_{\text {折}}\right)$$
  • 满载率约束
$$\max _{j}\left(\sum_{d=j+1}^{n} \sum_{o=1}^{j} q_{o d} / \sum_{i=1}^{2} f_{i} \cdot \sum_{d=1}^{j} \sum_{o=j+1}^{n} q_{o d} / \sum_{i=1}^{2} f_{i}\right) \leq \alpha \cdot C_z$$
  • 满足最小追踪间隔
$$f_{1}+f_{2} \leq \frac{3600}{I_{0}}$$
  • 折返站折返能力
$$f_1\le\frac{3600}{t_{折}}\\f_2\le\frac{3600}{t_折}$$
  • 满足最小发车频率
$$f_1>=f_{min}$$
  • 其他约束
    $$f_i\in N\ 1\le a<b\le n$$

2️⃣ MATLAB程序

所有的程序以及数据，OD出行矩阵以及区间运行时间在：列车交路方案优化遗传算法程序

2️⃣.1️⃣ myself.m——主脚本

主脚本，OD矩阵可以使用od.m脚本随机生成。

clear;clc;close all;

%% 生成随机OD矩阵
%od()

%%遗传参数设置
NUMPOP=200;%初始种群大小
irange_l=1; %问题解区间
irange_r=35; 
LENGTH=24; %二进制编码长度
ITERATION = 10000;%迭代次数
CROSSOVERRATE = 0.8;%杂交率
SELECTRATE = 0.4;%选择率
VARIATIONRATE = 0.2;%变异率
OD = xlsread('OD.xlsx');% 苏州地铁2号线调查问卷OD出行矩阵
h = xlsread('区间运行时间.xlsx'); % 苏州地铁2号线区间长度及运行时分

%初始化种群
pop=m_InitPop(NUMPOP,irange_l,irange_r);
pop_save=pop;
fitness_concat = [];
best_solution = [];
%开始迭代
for time=1:ITERATION
    %计算初始种群的适应度
    fitness=m_Fitness(pop, OD, h);
    fitness_concat = [fitness_concat;max(fitness)];
    pop_T = pop';
    [m,index] = max(m_Fitness(pop, OD, h));
   best_solution = [best_solution;pop(:,index)'];
    %选择
    pop=m_Select(fitness,pop,SELECTRATE);
    %编码
    binpop=m_Coding(pop,LENGTH,irange_l);
    %交叉
    kidsPop = crossover(binpop,NUMPOP,CROSSOVERRATE);
    %变异
    kidsPop = Variation(kidsPop,VARIATIONRATE);
    %解码
    kidsPop=m_Incoding(kidsPop,irange_l);
    %更新种群
    pop=[pop kidsPop];
end

disp(['最优解：' num2str(min(m_Fx(pop,OD))) '分钟']);
disp(['最优解对应的各参数：' num2str(pop(1,1)) ',' num2str(pop(2,1)) ',' num2str(pop(3,1)) ',' num2str(pop(4,1)) ]);
disp(['最大适应度：' num2str(max(m_Fitness(pop, OD, h)))]);   
    
figure
% set(gca,'looseInset',[0 0 0 0]);
set(gcf,'outerposition',get(0,'screensize'));
loglog(1:ITERATION, fitness_concat, 'Blue*-','linewidth',2)
legend('{\bf最优适应度值}');
xlabel('{\bf进化代数}','fontsize',30);
ylabel('{\bf最优适应度}','fontsize',30);
set(gca,'FontSize',20,'Fontname', 'Times New Roman');
set(get(gca,'XLabel'),'Fontsize',20,'Fontname', '宋体');
set(get(gca,'YLabel'),'Fontsize',20,'Fontname', '宋体');
set(get(gca,'legend'),'Fontsize',20,'Fontname', '宋体');
set(get(gca,'title'),'Fontsize',20,'Fontname', '宋体');
set(gca,'linewidth',2); 
print(gcf,'-dpng','-r300','最优适应度值-进化代数');

figure
% set(gca,'looseInset',[0 0 0 0]);
set(gcf,'outerposition',get(0,'screensize'));
semilogx(1 : ITERATION, best_solution,'linewidth',4)
legend('{\bf大小交路折返站a}','{\bf大小交路折返站b}','{\bf大交路发车频率f_1}','{\bf小交路发车频率f_2}');
% text(6, 0.3, '$\leftarrow  y= 2^{-x}$', 'HorizontalAlignment', 'left', 'Interpreter', 'latex', 'FontSize', 15);
xlabel('{\bf进化代数}','fontsize',15);
ylabel('{\bf参数各代最优值}','fontsize',15);
set(gca,'FontSize',20,'Fontname', 'Times New Roman');
set(get(gca,'XLabel'),'Fontsize',20,'Fontname', '宋体');
set(get(gca,'YLabel'),'Fontsize',20,'Fontname', '宋体');
set(get(gca,'legend'),'Fontsize',20,'Fontname', '宋体');
set(get(gca,'title'),'Fontsize',20,'Fontname', '宋体');
set(gca,'linewidth',2); 
print(gcf,'-dpng','-r300','参数各代最优值-进化代数');

2️⃣.2️⃣ od.m——生成随机出行OD矩阵

用来生成随机出行OD矩阵。

Mu = 26;
sigma = 10;
N = round(normrnd(Mu, sigma, [35 35]));
N = N + abs(min(N));
sum(sum(N))
if sum(sum(N)) > 35000 ;
    if sum(sum(N)) < 40000;
        xlswrite('test.xlsx',N,'Sheet1')
    end
end

2️⃣.3️⃣ m_InitPop.m——初始化种群

function pop=m_InitPop(numpop,irange_l,irange_r)
%% 初始化种群
%  输入：numpop--种群大小；
%       [irange_l,irange_r]--初始种群所在的区间
pop=[];
for j = 1:numpop
    for i=1:4
        % 因为a,b,f1,f2要求整数，所以生成随机整数
        pop(i,j)= round(irange_l+(irange_r-irange_l)*rand);
    end
end

2️⃣.4️⃣ m_Select.m——选择

function parentPop=m_Select(matrixFitness,pop,SELECTRATE)
%% 选择
% 输入：matrixFitness--适应度矩阵
%      pop--初始种群
%      SELECTRATE--选择率

sumFitness=sum(matrixFitness(:));%计算所有种群的适应度

accP=cumsum(matrixFitness/sumFitness);%累积概率
%轮盘赌选择算法
for n=1:round(SELECTRATE*size(pop,2))
    matrix=find(accP>rand); %找到比随机数大的累积概率
    if isempty(matrix)
        continue
    end
    parentPop(:,n)=pop(:,matrix(1));%将首个比随机数大的累积概率的位置的个体遗传下去
end
end

2️⃣.5️⃣ Crossover.m——交叉

%% 子函数
%
%题  目：Crossover
%
%%
%输   入：
%           parentsPop       上一代种群
%           NUMPOP           种群大小
%           CROSSOVERRATE    交叉率
%输   出：
%           kidsPop          下一代种群
%
%% 
function kidsPop = Crossover(parentsPop,NUMPOP,CROSSOVERRATE)
kidsPop = {[]};n = 1;
while size(kidsPop,2)<NUMPOP-size(parentsPop,2)
    %选择出交叉的父代和母代
    father = parentsPop{1,ceil((size(parentsPop,2)-1)*rand)+1};
    mother = parentsPop{1,ceil((size(parentsPop,2)-1)*rand)+1};
    %随机产生交叉位置
    crossLocation = ceil((length(father)-1)*rand)+1;
    %如果随即数比交叉率低，就杂交
    if rand<CROSSOVERRATE
        father(1,crossLocation:end) = mother(1,crossLocation:end);
        kidsPop{n} = father;
        n = n+1;
    end
end

2️⃣.6️⃣ Variation.m——变异

%% 子函数
%
%题  目：Variation
%
%
%输   入：
%           pop              种群
%           VARIATIONRATE    变异率
%输   出：
%           pop              变异后的种群
%% 
function kidsPop = Variation(kidsPop,VARIATIONRATE)
for n=1:size(kidsPop,2)
    if rand<VARIATIONRATE
        temp = kidsPop{n};
        %找到变异位置
        location = ceil(length(temp)*rand);
        temp = [temp(1:location-1) num2str(~temp(location))...
            temp(location+1:end)];
       kidsPop{n} = temp;
    end
end

2️⃣.7️⃣ m_Coding.m——编码

因为总共$35$座车站，$a,b,f_1,f_2$都不超过$35<2^6$，所以$4$个参数都设置为$6$位二进制，这样编码总长度为$24$。

function binPop=m_Coding(pop,pop_length,irange_l)
%% 二进制编码（生成染色体）
% 输入：pop--种群
%      pop_length--编码长度
for n=1:size(pop,2) %列循环
    binPop{n} = '';
    for k=1:size(pop,1) %行循环
        substr = dec2bin(pop(k,n));
        lengthpop = length(substr);
        for s = 1:6-lengthpop
            substr = ['0' substr];
        end
        binPop{n} = [binPop{n} substr];
    end
end

2️⃣.8️⃣ m_Incoding.m——解码

解码时编码长度为$24$，每隔$6$位转化成十进制。

function pop=m_Incoding(binPop,irange_l)
%% 解码
popNum=1;
popNum = 4;%染色体包含的参数数量
for n=1:size(binPop,2)
    % 因为有35个车站，35<2^6 ，所以编码为6位
    pop(1,n) = bin2dec(binPop{1,n}(1:6)); 
    pop(2,n) = bin2dec(binPop{1,n}(7:12));
    pop(3,n) = bin2dec(binPop{1,n}(13:18));
    pop(4,n) = bin2dec(binPop{1,n}(19:24));
end
% pop = pop./10^6+irange_l;

2️⃣.9️⃣ m_Fitness.m——适应度函数(重要，实现约束条件)

在这里实现约束条件，思路就是不满足约束条件的种群的适应度设置为无穷小，那么在下一代的迭代中就会将适应度低的种群淘汰掉，实现约束的目的。

function fitness=m_Fitness(pop, OD, h)
%% Fitness Function
for n=1:size(pop,2)
    a = pop(1,n);
    b = pop(2,n);
    f1 = pop(3,n);
    f2 = pop(4,n);
%% 约束条件，不满足约束则适应度值无穷小    
 %% 1) a,b,f1,f2 不能为0
    if a == 0 || b == 0 || f1 == 0 || f2 == 0
        fitness(n) = 1/1000000000;
        continue;
    end
 %% 2) a,b,f1,f2 不能超过35
    if a > 35 || b > 35 || f1 >35 || f2 >35 
         fitness(n) = 1/1000000000;
        continue;
    end
%% 3) 列车数量约束
     if (sum(h) * 120 + 1170) *( f1 - 16) + (sum(h(a: b-1)) + (b - a + 1) * 30 + 120) * f2 > 0
        fitness(n) = 1/1000000000;
        continue;
     end
%% 4) 满载率约束   
%     constraint2 = [];
%     for j = 2:33
%         constraint2(j) = (sum(sum(OD(1:j, j+1:35)))/(f1+f2)) * (sum(sum(OD(j+1:35,1:j)))/(f1+f2));
%     end
%     if max(constraint2) > 1 * 1460
%         fitness(n) = 1/1000000000;
%         continue;
%     end
%% 5) 最小追踪间隔     
    if f1 + f2 > 30
        fitness(n) = 1/1000000000;
        continue;
    end 
%% 5) 最小发车间隔   
    if f1 < 12
          fitness(n) = 1/1000000000;
           continue;
    end
%% 主要适应度函数，设置为目标函数的倒数，即目标函数要求最小，那么越小，适应度就越大    
    fitness(n)= 1/m_Fx(pop(:,n), OD);
end

2️⃣.🔟 m_Fx.m——目标函数(重要)

function y=m_Fx(x, OD)
%% 要求解的函数
%% Z = Q1 * t1d + Q2 * t2d
    y = (sum(sum(OD)) - sum(sum(OD(x(1):x(2),x(1):x(2))))) * (30/x(3)) + sum(sum(OD(x(1):x(2),x(1):x(2)))) * (30/(x(3)+x(4)));
end

3️⃣ 运行结果

最优解：71335.4762分钟
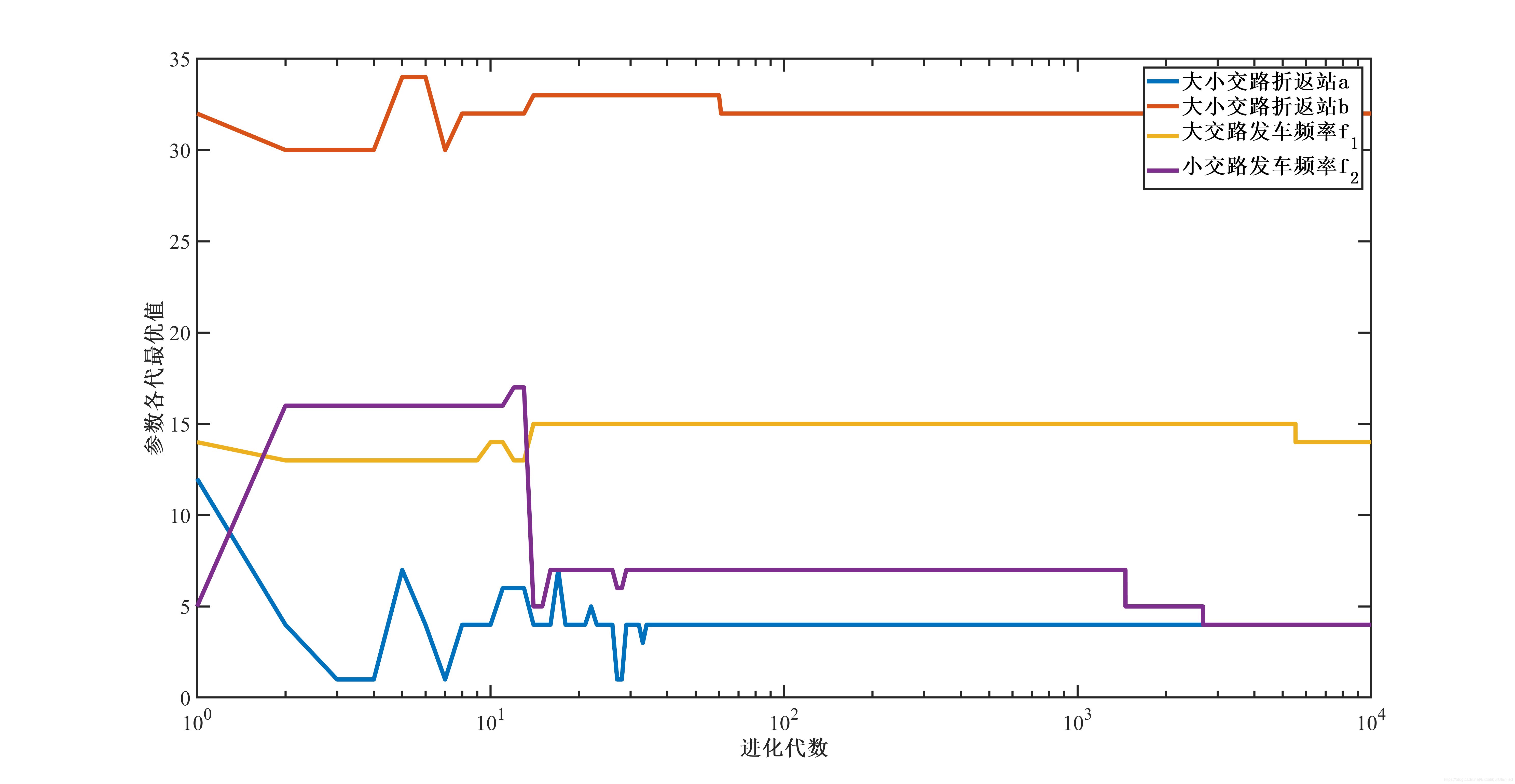
最优解对应的各参数：4,32,14,4
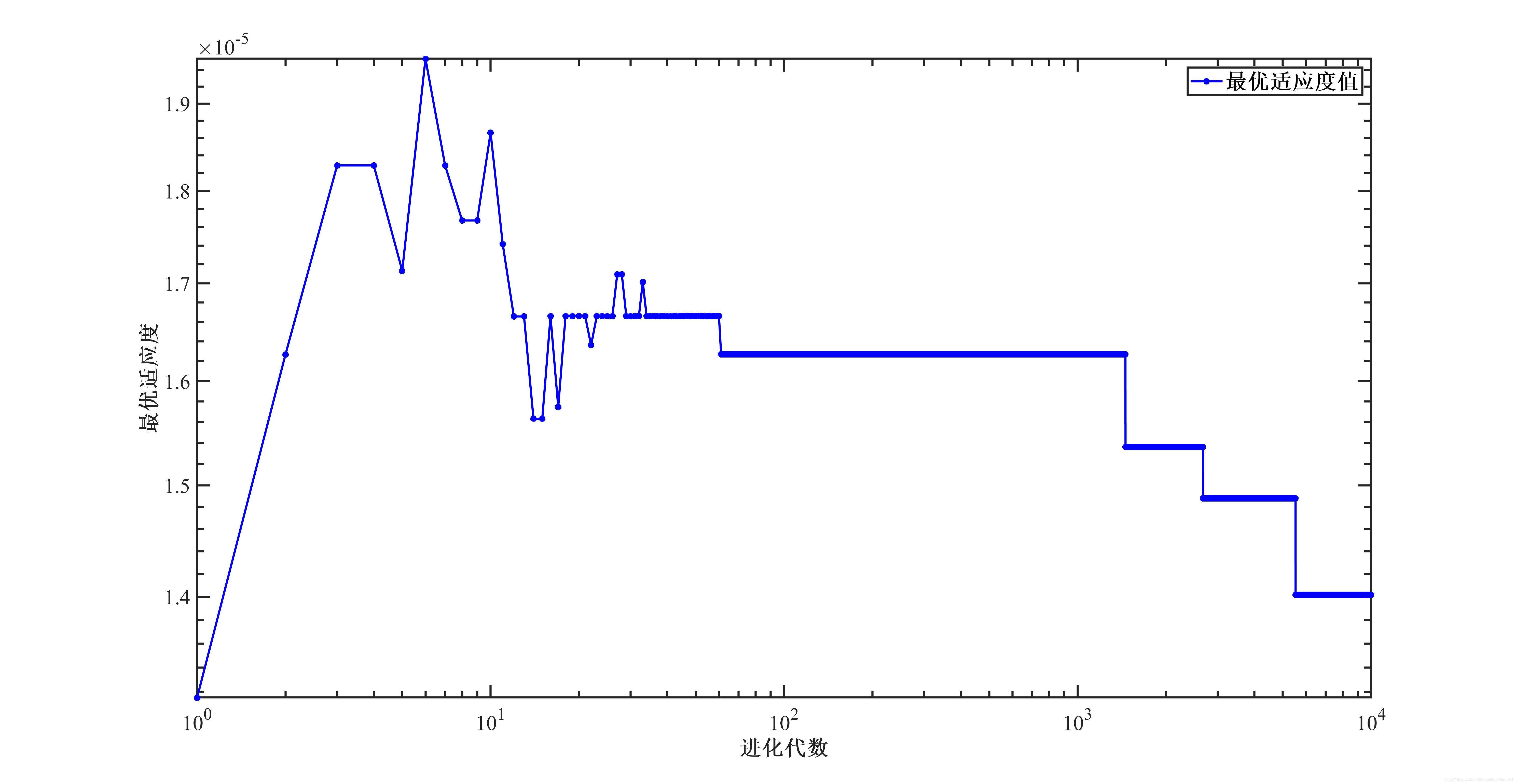
最大适应度：1.4018e-05

即设置第$4$和第$32$个站点为大小交路折返站，大交路发车频率为$14$列/小时，小交路发车频率为$4$列/小时，最低平均等待时间为$71335$分钟。

图像结果：
在这里插入图片描述
在这里插入图片描述

0
MATLAB
版权归属： Excalibur
本文链接： https://kemo.xyz/archives/de-tie-da-xiao-jiao-lu-you-hua-mo-xing-de-yi-chuan-suan-fa-qiu-jie
许可协议： 本文使用《署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0)》协议授权

评论区